我有个兄弟,是抖音的点赞狂魔,他的点赞次数高达6924次,而且他大多数的赞都是给那些青春靓丽的小姐姐们,如下图。看他的抖音推荐内容,都是满目的小姐姐唱啊跳啊不亦乐乎,他也觉得甚爽。不过,好景不长,没多久他就跟我说:“我再也不敢再点了,我老婆已经发现我给小姐姐们点了上1000个赞,而且知道我点赞的视频,也会推荐给她”。
把好友看过的视频推荐给用户,这就是协同过滤。准确地说,叫用户协同过滤(User Collaborative Filtering)。
一、协同过滤概述(Collaborative Filtering)
协同过滤(简称CF)是推荐系统最重要的思想之一。在早期,协同过滤几乎等同于推荐系统。协同过滤思想产生于1994年,被用于邮件系统上。2001年,亚马逊用协同过滤算法来推荐相似商品。
协同过滤的思想比较简单,主要有三种:
用户协同过滤(UserCF):相似的用户可能喜欢相同物品。如加了好友的两个用户,或者点击行为类似的用户被视为相似用户。如我兄弟和她的太太互加了抖音好友,他们两人各自喜欢的视频,可能会产生互相推荐。
物品协同过滤(ItemCF):相似的物品可能被同个用户喜欢。这个就是著名的世界杯期间沃尔玛尿布和啤酒的故事了。这里因为世界杯期间,奶爸要喝啤酒看球,又要带娃,啤酒和尿布同时被奶爸所需要,也就是相似商品,可以放在一起销售。
模型协同过滤:使用矩阵分解模型来学习用户和物品的协同过滤信息。一般这种协同过滤模型有:SVD,SVD++等。这种协同过滤要比前两个来得抽象些,这里先不解释,后面详述。
下面按照物品协同过滤,用户协同过滤和模型协同过滤的顺序,详细解释这几种算法。
二、物品协同过滤的计算
2003年,亚马逊发表了一篇论文,阐述了他们如何用物品协同过滤算法(Item-to-Item Collaborative Filtering),搭建他们“看了又看”功能。如下图:
这是17年前的截图,图跟纸质老照片那样变得斑驳。图中是在购物车关联页面的相关推荐。那么,这个协同过滤推荐是如何做计算出来的呢?
前面第一章说到,人工智能实践过程三个步骤:数据,学习和决策。这里也将用同样步骤,以图书销售推荐为例,解释物品协同过滤的过程。为了简单化,假设某图书销售平台总共有6本书销售,有6个用户购买。
数据:用户的评分数据,分值1-5分。每个用户对图书的评分如下图矩阵所示。
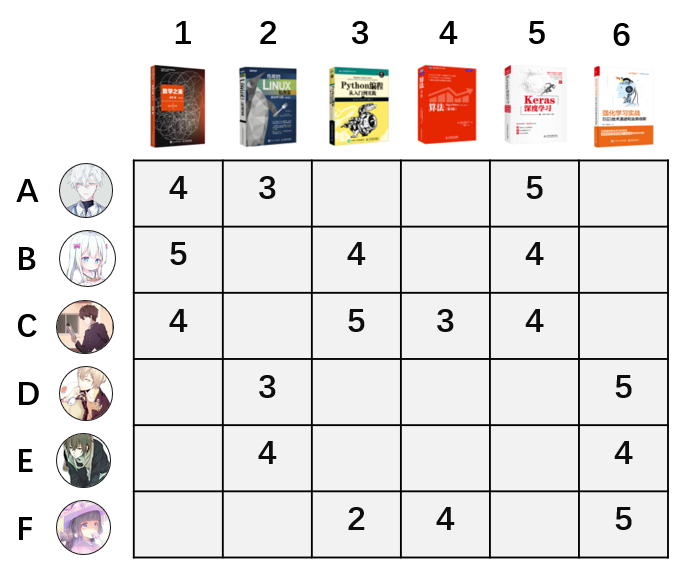

学习算法:前面说到ItemCF的定义是,相似的物品可能被同个用户喜欢。反过来讲,就是被同个用户喜欢的物品是相似商品。如上图中,图书1和图书2两本书,被用户A同时喜欢,这两本书具有相似性。而图书5和图书6,没有被同个用户同时喜欢,不具有相似性。
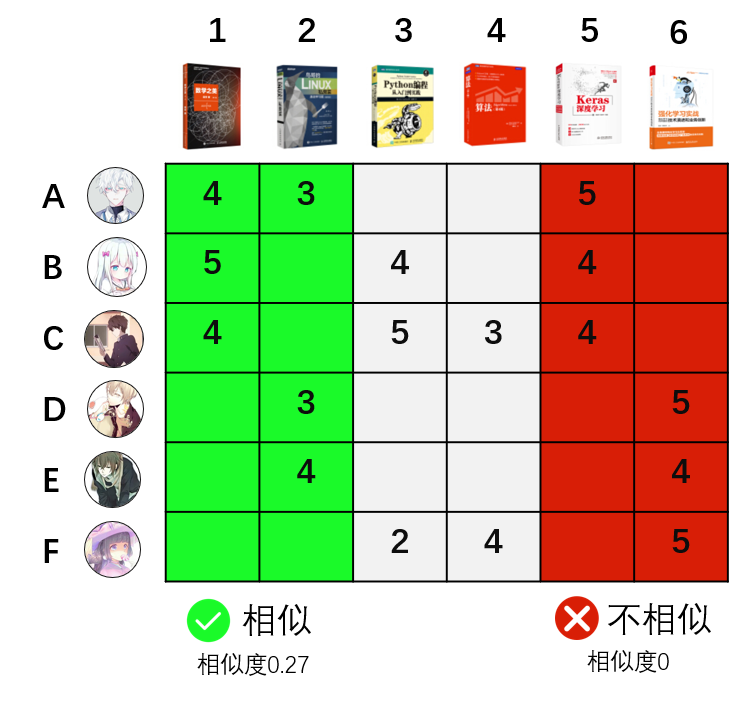
如果用余弦相似度计算图书1和图书2的相似度,也叫做cosine距离,计算过程为:
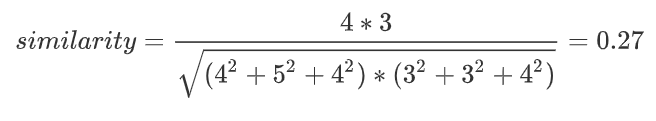
回想高中时候的课本我们就可以知道,上面的similarity计算公式,实际上就是计算书籍1的评分向量(4,5,4,0,0,0)和书籍2的评分向量(3,0,3,3,4,0)的 cos 夹角。
用同样的方式,可以算出图书1跟其他五本图书相似度分别为0.27, 0 .79,0.32,0.99和0。对每两本书计算完这个相似度后,就可以获得全部图书的相似矩阵。


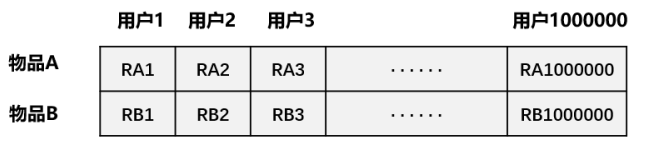
一个平台不仅仅有6本图书6个用户,我们再扩展到一般的情况。计算物品的相似度,实际是计算每两个物品评分向量的cosine距离,评分向量的每一维,代表了一个用户,下图中,表格的第一行代表了所有用户对物品A的评分。当有100万个用户时,也就是计算每两个100万维向量的距离。这样就导致计算量很大,而且很多平台不仅仅只有100万用户,因而这个低效的计算方式需要改进。

预测决策:
有了评分矩阵之后,预测决策一般有两种场景。
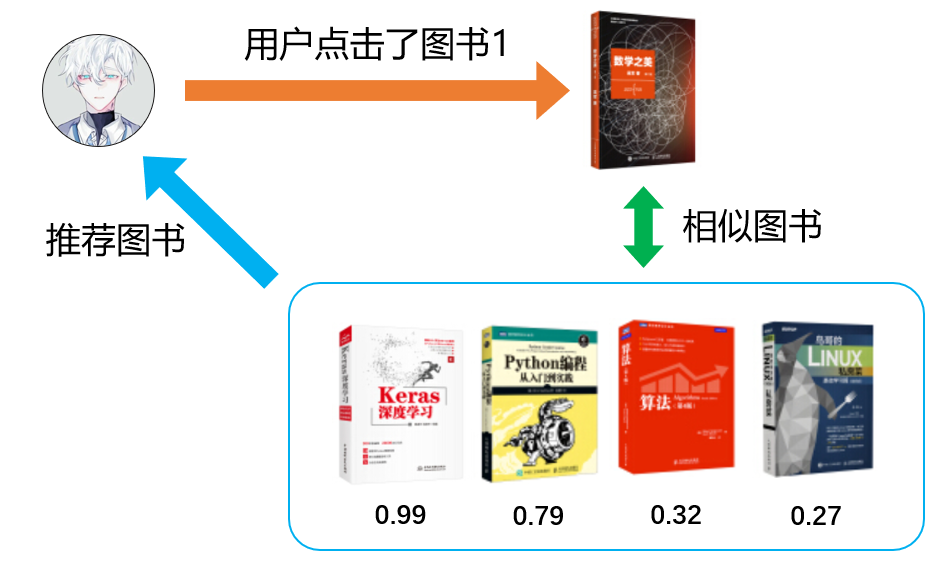
一种是根据相似度排序推荐最近邻物品。类似于“看了还看”,“买了还买”场景。在这里的例子中,我们知道图书1和其他图书的相似度排序分别是图书5,图书3,图书4和图书2。当用户点击了图书1时,就可以按照相似顺序从高到低推荐。

第二种是根据相似度预测评分推荐物品。如何决策要不要给用户B推荐图书2,图书4和图书6呢?如下图,通过用户B对图书1的评分 * 未知图书与图书1的相似度来预测用户B对剩下图书的评分。如图书2的预测评分 = 图书1的评分5分 * 图书1和图书2的相似度0.27 ,从而用户B对图书2的评分是:5*0.27=1.35。同样方式计算出其他图书的评分预测。

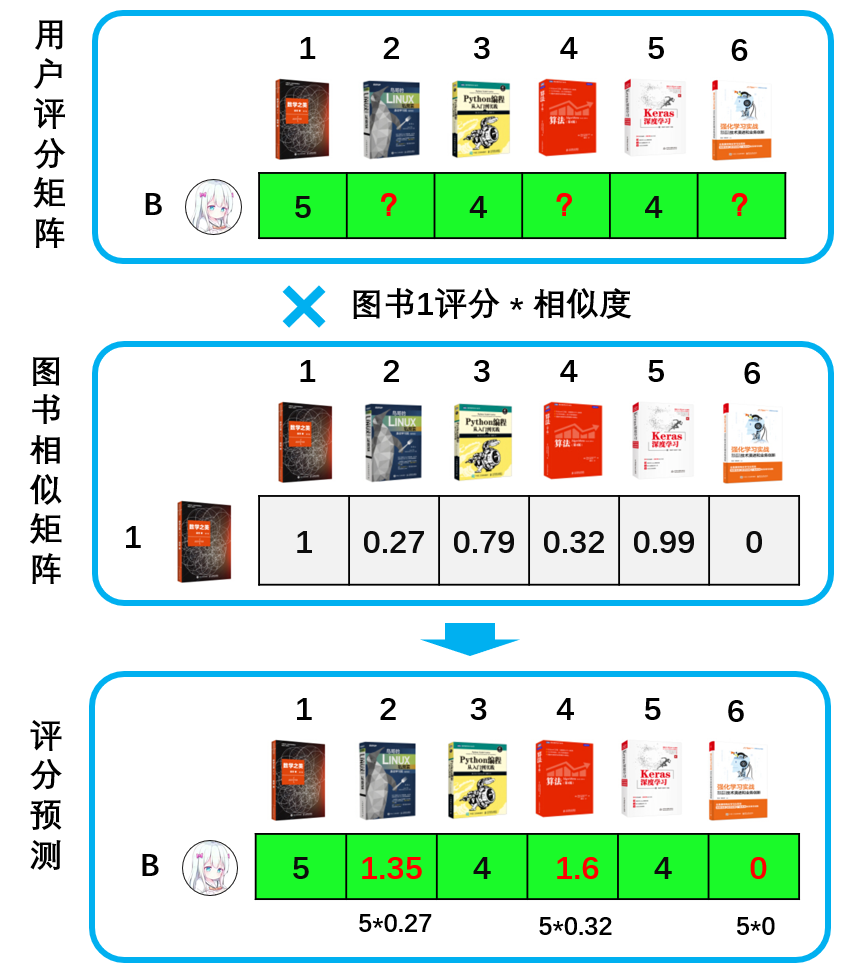
从上面的结果来看,用户B对其他图书评分比较低,这几本图书推荐的可能性大大减少。
物品协同过滤实际使用
这是推荐系统里最朴素的算法,因为它的计算量会随着用户和物品的数量呈指数增长,所以它并不适合在大量用户或大量物品的场景使用。在它诞生的年代,还没有大数据,这种计算方式耗费大量内存,需要做大量的优化。我尝试过用100万用户,100万物品和500万条的数据在256G内存的机器上做过尝试,计算一分钟后就宣告内存耗尽。确实需要计算的话,一般使用Spark来实现。
因为这个缺点,就需要新的算法来计算物品的协同过滤。
前面提到,计算任意两物品之间的相似度后,有两个使用场景。针对这两个场景,分别有不同的迭代算法:
- 根据相似度排序推荐最近邻物品:使用如Word2vec,Item2vec等Embedding类的算法,将物品嵌入固定的向量空间中,再使用LSH算法(局部敏感哈希算法)取最近邻物品。这个后续文章会介绍。
- 根据相似度预测评分推荐物品:本章后续介绍的SVD算法。
虽然这个算法使用较少了,但是物品协同过滤的思想都是一脉相乘的,理解了这个简单的cosine相似度计算方式,可以更好理解后续的迭代算法。
最后补充一下,物品协同过滤的一个缺点,或者说是协同过滤的缺点,对于一个新物品,协同过滤是无法推荐的。因为新物品用户无评分,导致它跟所有物品的相似度都是为0。这个是使用这个算法时非常需要注意的一个点。
三、用户协同过滤计算
用户协同过滤(UserCF)的计算方式跟物品协同过滤(ItemCF)的计算方式类似。不同的是由计算两两物品的相似度,转换成计算两两用户的相似度。如下图所示:
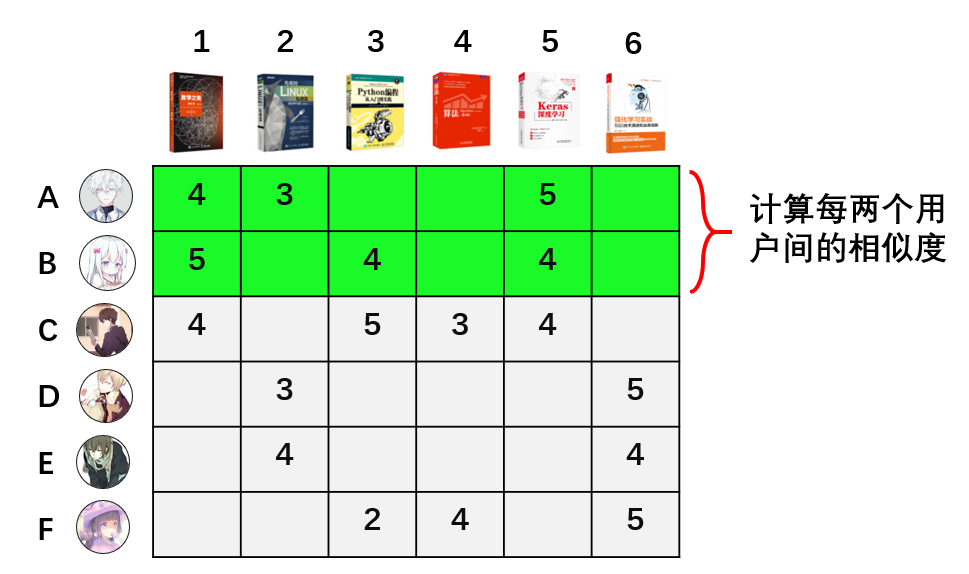

评分了相同图书的用户为相似用户,他们的相似度同样也用cosine相似度公式来计算。计算完相似度后,就可以根据用户间的相似性,预测用户对未评分图书进行评分预测。
但是在亚马逊上,由于用户评分的稀疏性(很多用户压根不评分),没有评分的用户无法跟其他用户计算相似性,从而导致很多用户之间没有相似度。所以2001年的时候,亚马逊选择物品协同过滤算法来做推荐,并发表了论文。这个论文也导致大家一度认为物品协同过滤优于用户协同过滤。
其实只有最合适的算法,没有最优的算法
时间到了移动互联网的今天,我们更多是用点击数据,用户好友关系,通讯录或者甚至是同一个WIFI地址来计算用户协同过滤,数据稀疏性得到一定程度上的解决。现在,用户的协同过滤在信息流内容推荐,社交性的推荐系统有着很好的利用。比如抖音,因为内容更新频繁,用户协同过滤可以作为很好的召回手段,所以也就会出现老公点赞的视频会被推荐给他老婆的情景。
同样地,这里介绍的cosine相似度的算法,也不是工业界现在最佳实践的用户相似度计算方式了。用户相似度的计算,现在的最佳实践也同样也是用Embedding的方式实现。
而且,用户相似度的计算,最有效的方式不一定是通过本节中介绍的计算方式,带社交功能的APP可以通过用户的好友关系,一般的APP可以通过获取用户的通讯录实现用户协同过滤。这些方式都来的更加简单和直接。
四、模型协同过滤-矩阵分解(SVD)
对于很多没有计算机专业背景的人来说,直接理解SVD算法是很困难的。需要有高等数学,线性代数,还要理解机器学习模型中的目标函数,损失函数,梯度,正则化,最小二乘法等概念。很多文章介绍SVD都很技术,这里不准备采用技术大咖们的方式。我还是继续用图文的方式介绍,这也许是世界上最简单的理解SVD的方式。
首先介绍一下背景。
SVD算法的诞生,跟美国Netflix公司有关。这家公司中文名叫网飞,拍了大家熟悉的网剧《纸牌屋》。


时间来到2006年,Netflix发起一个推荐系统的悬赏竞赛。他们公开了自己网站的用户数据评分数据包,并放出100万美元悬赏优化推荐算法。凡是能在Netflix现有的推荐系统基础上,把均方根误差降低10%的人,都能参与瓜分这100万美元。消息一放出,引来了无数高手参加。这场比赛中,最佳算法就是SVD。
背景介绍完了,接下来直接介绍SVD是怎么计算的。
还是跟前面那样,简单化问题:假设一个平台只有4个用户和4本图书。
1、数据:用户对物品评分1-5分,且有以下评分记录。

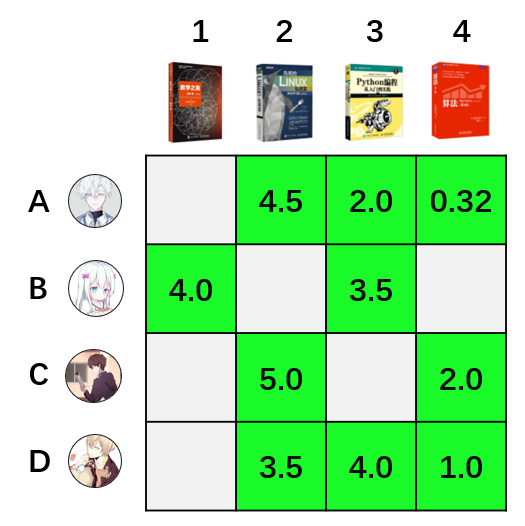
2、学习算法:
根据线性代数我们知道,一个矩阵可以分解为多个矩阵的乘积。SVD英文全称叫做Singular Value Decomposition,这个算法是个矩阵分解的通用名称,在不同领域有不同的形式。在推荐系统领域,可以简单的认为,SVD就是将一个矩阵,在一定的精度损失下,将一个矩阵分解成两个矩阵。运用这个算法,我们可以将上图的矩阵做以下的近似分解:

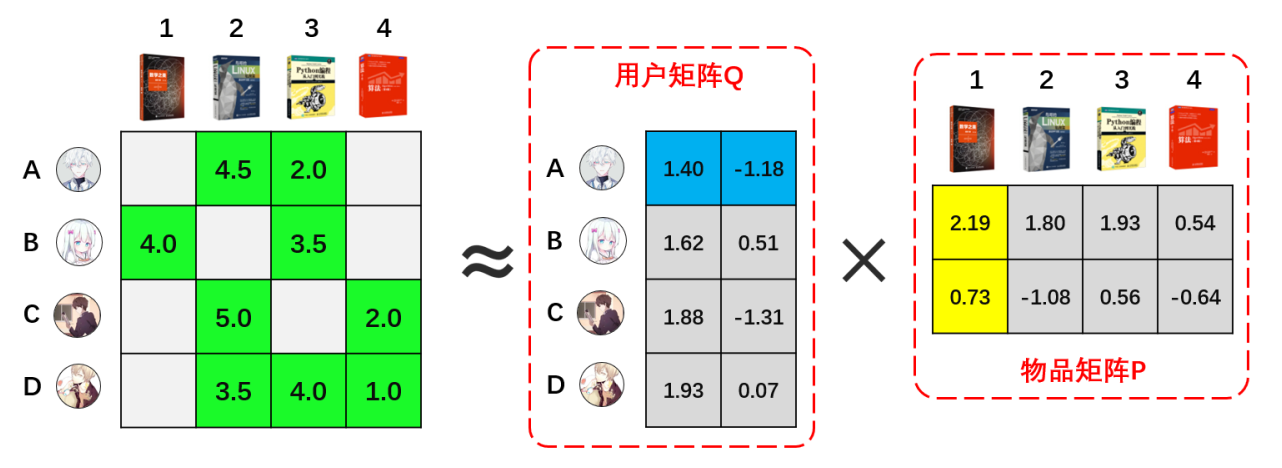
其中,用户矩阵部分代表着每个用户的偏好在一个二维隐语义空间上的映射。同样地,物品矩阵代表着每本图书的特性在一个二维隐语义空间上的映射。这两个矩阵也就是模型的结果。这样,我们训练模型的时候,就只需要训练用户矩阵中的8个参数和物品矩阵中的8个参数即可。大大减少了计算量。
模型训练的过程,简单地说,就是通过最小二乘法,不断将用户评分数据迭代入矩阵中计算,直到把均方误差优化到最小。上图的结果是我通过Spark的ML库ALS模块直接计算的。
算法的具体目标函数,损失函数和梯度等,详述则涉及很多机器学习知识点,这里就不作介绍了。技术方面有很多解读文章,需要进一步理解的同学,可以搜索相关文章阅读。
3、预测决策:
通过模型训练,我们得到用户矩阵Q和物品矩阵P后,全部用户对全部图书的评分预测可以通过R = PQ来获得。如上图中,用户A的向量(1.40,-1.18)乘以物品2的向量(2.19,0.73)则可得用户A对物品1的评分预测为:1.40×(-1.18)+2.19×0.73=2.21。
对所有的用户和物品都执行相同操作,可以得到全部用户对全部物品的评分。如下图右侧矩阵:
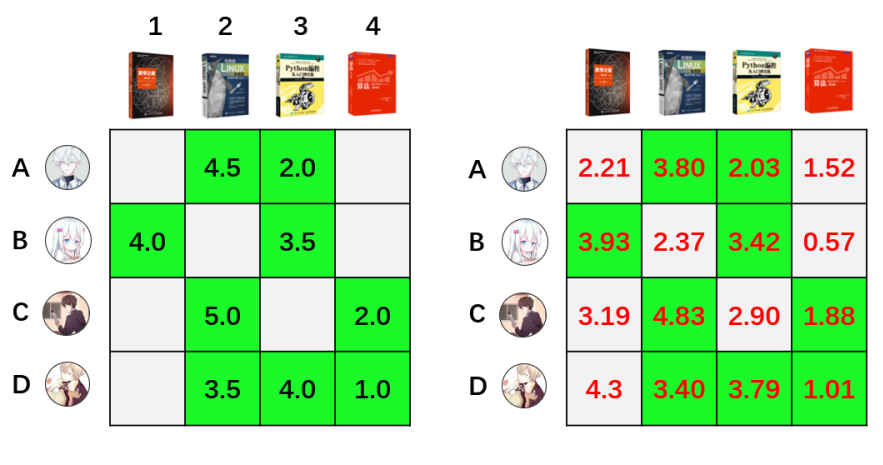
得到全部的评分预测后,我们就可以对每本图书进行择优推荐。需要注意的是,用户矩阵和物品矩阵的乘积,得到的评分预估值,与用户的实际评分不是全等关系,而是近似相等的关系。如上图中两个矩阵绿色部分,用户实际评分和预估评分都是近似的,有一定的误差。
在现在的实际应用中,SVD一般作为协同过滤的离线召回使用。一般地,将需要给用户推荐的物品提前离线计算好,存在HBASE中,在用户有请求的时候,直接读取推荐的结果,放入初排阶段的召回集中。
五、总结
1、协同过滤优点:
协同推荐是应用最广泛的推荐算法。基于内容推荐的算法,需要给物品打上标签和给用户建用户画像,才能实现匹配推荐。相比之下,协同过滤简单了许多。它是仅使用用户行为的进行推荐,我们不需要对物品或信息进行完整的标签化分析,避免了一些人可能难以量化描述的概念的标签构建,又可以很好地发现用户的潜在兴趣偏好。
2、协同过滤缺点:
因为协同过滤依赖用户的历史数据,面对新的用户或者新的物品,在开始的时候没有数据或数据较少时,协同过滤算法无法做出推荐。需要等数据积累,或者其他方案进行弥补缺陷,也就是常说的冷启动的问题。
3、机器学习领域
当精确的方式不行难以计算或者速度太慢的时候,往往会选择牺牲一点精度,达到差不多但非常快速的效果。SVD就是其中的一个例子。
4、没有完美的算法,只有最合适的算法
现在的实践,也不是单纯用协同过滤来做推荐,而是将他们作为其中的一个或几个召回策略来使用。
作者: 菠萝王子
