
最适解法是由美国的戴维·米勒(D.W.Miller)和斯塔(M.R.Star)两人在1964年与杨·罗比凯广告公司(Y&R)共同研制开发的,它是利用线性规划作为媒体选择模式。
最适解法是利用线性模式,从限定的广告预算中,选取最佳的广告媒体组合。但是,模式中的假设与实际有较大出入,如媒体的反复效果每次并不一样,每次广告的媒体费用也不同,而且也没有考虑到媒体间重复到达目标市场等问题。因为这种模式与媒体运用的实际情况有较大出入,人们又采用非线性规划法对其进行了改善。
最适解法模型
进行广告媒体策划,为使广告效果最好,往往要受多种因素限定条件的约束,如广告预算、媒体的使用单位等,数学规划提供了解决这类问题的有效方法。数学规划模型主要由三个部分构成:目标函数的极大化或极小化;有一组约束条件;决策变量取非负值。
最适解法是数学规划中线性规划模型的一个应用特例。根据广告媒体的实际情况,可将线性规划模型修改变为:求广告效果及这一目标函数极大化;受约束于广告预算的数量;若以决策变量Xi表示购买第i种媒体的次数,则X_i</math>不能小于该媒体的最小单位数,亦不可大于该媒体的最大单位数,那么广告媒体策划最适解法的数学模型可表述如下:
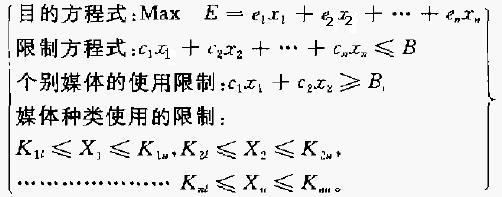
最适解法
其中:E表示总暴露频次;ei表示在i媒体一次广告的暴露频次;xi表示在i媒体做广告次数;ci表示在i媒体做一次广告的成本费用;B表示广告主的广告预算总额;B1且表示广告预算中的一部分;Ki表示购买第i媒体的最小单位数;Ki表示购买第i媒体的最大单位。
